L'umidificatore che va a gatti

Roma – Umidificare l’ambiente è di fondamentale importanza, soprattutto lì dove sono in funzione i vecchi termosifoni, capaci di riscaldare le stanze, ma anche di seccare l’aria, provocando non pochi fastidi respiratori.
Per ovviare, esistono diversi tipi di umidificatori ambientali, di cui alcuni passivi, mentre altri sono alimentati dalla corrente elettrica. Il designer cinese Yuan Gu ha progettato un concept di umidificatore alquanto particolare: si tratta della Wool Ball, un gadget elettronico a forma di gomitolo di lana, con la quale è possibile umidificare l’ambiente in due differenti modalità, standard o ibrida.

La modalità standard prevede che l’umidificatore dalla forma tondeggiante lavori collegato alla presa elettrica dell’ambiente da umidificare, in modo che venga alimentato direttamente dall’impianto elettrico di casa. E fino a qui, nulla di speciale.

La modalità ibrida, invece, è la più sorprendente: durante il funzionamento l’umidificatore riceve l’alimentazione per funzionare direttamente da una batteria integrata, che però continua a ricaricarsi anche lontano dalla presa a muro, semplicemente attraverso il movimento della palla, che magari viene usata dal gatto o dal cane di casa per giocare. Ogni rotazione della Wool Ball, consente alla batteria di accumulare dell’energia proveniente dal generatore interno, attivato proprio dal movimento.

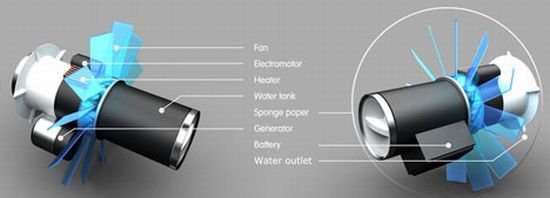
Inoltre, il dispositivo sarebbe completo di un display LCD che permette all’utente di avere una facile lettura sullo stato di carica della batteria integrata nel gadget.

Il concept sembra sia stato creato per l’azienda cinese di umidificatori “YADU”, appositamente per il mercato nordamericano.
Un’idea felina, si potrebbe pensare, ma se al gatto dovesse non piacere il giocattolo e lo boicottasse?

( via GIZMODO )